Методы вычисления обратной матрицы. Обратная матрица онлайн. Метод обратной матрицы
Обратная матрица — это матрица A −1 , при умножении на которую заданная начальная матрица A даёт в итоге единичную матрицу E :
АA −1 = A −1 A = E.
Метод обратной матрицы.
Метод обратной матрицы - это один из самых распространенных методов решения матриц и применяется для решения систем линейных алгебраических уравнений (СЛАУ) в случаях, когда число неизвестных соответствует количеству уравнений.
Пусть есть система n линейных уравнений с n неизвестными:
Такую систему можно записать как матричное уравнение A* X = B ,
где  - матрица системы,
- матрица системы,
 - столбец неизвестных,
- столбец неизвестных,
 - столбец свободных коэффициентов.
- столбец свободных коэффициентов.
Из выведенного матричного уравнения выражаем X путем умножения обеих частей матричного уравнения слева на A -1 , в результате чего имеем:
A -1 * A * X = A -1 * B
Зная, что A -1 * A = E , тогда E * X = A -1 * B либо X = A -1 * B .
Следующим шагом определяется обратная матрица A -1 и умножается на столбец свободных членов B .
Обратная матрица к матрице A существует лишь тогда, когда det A ≠ 0 . Ввиду этого при решении СЛАУ методом обратной матрицы первым делом находится det A . Если det A ≠ 0 , то у системы есть только одно решение, которое можно получить методом обратной матрицы, если же det A = 0 , то такая система методом обратной матрицы не решается.
Решение обратной матрицы.
Последовательность действий для решения обратной матрицы :
- Получаем определитель матрицы A . Если определитель больше нуля, решаем обратную матрицы дальше, если он равен нулю, то здесь обратную матрицу найти не удастся.
- Находим транспонированную матрицу AT .
- Ищем алгебраические дополнения, после чего заменяем все элементы матрицы их алгебраическими дополнениями.
- Собираем обратную матрицу из алгебраических дополнений: все элементы полученной матрицы делим на определитель исходно заданной матрицы. Итоговая матрица будет искомой обратной матрицей относительно исходной.
Приведенный ниже алгоритм решения обратной матрицы по сути такой же, как и приведенный выше, разница только в нескольких шагах: первым делом определяем алгебраические дополнения, а уже после этого вычисляем союзную матрицу C .
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Вычисляем алгебраические дополнения.
- Составляем союзную (взаимную, присоединённую) матрицу C .
- Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
- Проверяем выполненную работу: умножаем начальную и полученную матрицы, результатом должна стать единичная матрица.
Это лучше всего делать с помощью присоединённой матрицы.
Теорема: Если к квадратной матрице с правой стороны приписать единичную матрицу такого же порядка и при помощи элементарных преобразований над строками преобразовать начальную матрицу, стоящую слева, в единичную, то полученная с правой стороны будет обратной к начальной.
Пример нахождения обратной матрицы.
Задание. Для матрицы ![]() найти обратную методом присоединенной матрицы
.
найти обратную методом присоединенной матрицы
.
Решение. Дописываем к заданной матрице А справа единичную матрицу 2го порядка:
![]()
Из 1й строки вычитаем 2ю:
![]()
От второй строки отнимаем 2 первых:
![]()
Как правило, обратные операции используются для упрощения сложных алгебраических выражений. Например, если в задаче присутствует операция деления на дробь, можно заменить ее операцией умножения на обратную дробь, что является обратной операцией. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.
Шаги
С помощью присоединенной матрицы
Транспонируйте исходную матрицу. Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.
- Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.
Найдите определить каждой матрицы размером 2х2. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.
- Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
- Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
- Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.
Создайте матрицу кофакторов. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.
- Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
- Подробную информацию о матрицах кофакторов можно найти в интернете.
- Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).
Разделите каждый элемент присоединенной матрицы на определитель. Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель. Результат каждой операции деления запишите там, где находится соответствующий элемент. Так вы найдете матрицу, обратную исходной.
- Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
- В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.
Запишите обратную матрицу. Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.
С помощью калькулятора
Выберите калькулятор, который работает с матрицами. С помощью простых калькуляторов нельзя найти обратную матрицу, но это можно сделать на хорошем графическом калькуляторе, таком как Texas Instruments TI-83 или TI-86.
Введите исходную матрицу в память калькулятора. Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2 nd и Matrix.
Выберите меню Edit (Редактирование). Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).
Введите обозначение матрицы. Большинство графических калькуляторов умеет работать с 3-10 матрицами, которые можно обозначить буквами А-J. Как правило, просто выберите [A], чтобы обозначить исходную матрицу. Затем нажмите кнопку Enter (Ввод).
Введите размер матрицы. В данной статье говорится о матрицах 3х3. Но графические калькуляторы умеют работать с матрицами больших размеров. Введите количество строк, нажмите кнопку Enter, затем введите количество столбцов и еще раз нажмите кнопку Enter.
Введите каждый элемент матрицы. На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.
Обратная матрица для данной это такая матрица, умножение исходной на которую дает единичную матрицу: Обязательным и достаточным условием наличия обратной матрицы является неравенство нулю детерминанта исходной (что в свою очередь подразумевает, что матрица должна быть квадратная). Если же определитель матрицы равняется нулю, то ее называют вырожденной и такая матрица не имеет обратной. В высшей математике обратные матрицы имеют важное значение и применяются для решения ряда задач. Например, на нахождении обратной матрицы построен матричный метод решения систем уравнений. Наш сервис сайт позволяет вычислять обратную матрицу онлайн двумя методами: методом Гаусса-Жордана и с помощью матрицы алгебраических дополнений. Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй - вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом - Вычисление детерминанта матрицы онлайн
.Найти обратную матрицу на сайт
сайт позволяет находить обратную матрицу онлайн быстро и бесплатно. На сайте произвордятся вычисления нашим сервисом и выдается результат с подробным решением по нахождению обратной матрицы . Сервер всегда выдает только точный и верный ответ. В задачах по определению обратной матрицы онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе сайт сообщит о невозможности найти обратную матрицу ввиду равенства нулю определителя исходной матрицы. Задача по нахождению обратной матрицы встречается во многих разделах математики, являясь одним из самых базовых понятий алгебры и математическим инструментом в прикладных задачах. Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Назначение сервиса. С помощью данного сервиса в онлайн режиме можно найти алгебраические дополнения, транспонированную матрицу AT, союзную матрицу и обратную матрицу.
Онлайн калькулятор. Обратная матрицы.
Решение проводится непосредственно на сайте (в онлайн режиме) и является бесплатным. Результаты вычислений оформляются в отчете формата Word и в формате Excel (т.е. имеется возможность проверить решение). см. пример оформления.
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Алгебраические дополнения.
1,1 = (-1 4-5 (-2)) = 6
1,2 = -(2 4-(-2 (-2))) = -4
1,3 = (2 5-(-2 (-1))) = 8
2,1 = -(2 4-5 3) = 7
2,2 = (-1 4-(-2 3)) = 2
2,3 = -(-1 5-(-2 2)) = 1
3,1 = (2 (-2)-(-1 3)) = -1
3,2 = -(-1 (-2)-2 3) = 4
3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу
можно записать как:
| A-1 = |
| 0,6 | -0,4 | 0,8 |
| 0,7 | 0,2 | 0,1 |
| -0,1 | 0,4 | -0,3 |
Нахождение обратной матрицы
Матрица А-1 называется обратной матрицей по отношению к матрице, если А*А-1 = , где - единичная матрица -го порядка. Обратная матрица может существовать только для квадратных матриц.
см. также Обратная матрица методом Жордано-Гаусса
Алгоритм нахождения обратной матрицы
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Нахождение транспонированной матрицы AT.
- Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Следующий алгоритм нахождения обратной матрицы аналогичен предыдущему за исключением некоторых шагов: сначала вычисляются алгебраические дополнения, а затем определяется союзная матрица.
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Определение алгебраических дополнений.
- Заполнение союзной (взаимной, присоединённой) матрицы.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент присоединённой матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Пример №1. Запишем матрицу в виде:
Обратная матрица существует, если определитель матрицы отличен от нуля. Найдем определитель матрицы:
= -1 (-1 4-(-2 5))-2 (2 4-(-2 (-2)))+3 (2 5-(-1 (-2))) = 10. Определитель равен 10 и не равен нулю. Продолжаем решение.
Найдем транспонированную матрицу:
Алгебраические дополнения.
1,1 = (-1 4-5 (-2)) = 6
1,2 = -(2 4-(-2 (-2))) = -4
1,3 = (2 5-(-2 (-1))) = 8
2,1 = -(2 4-5 3) = 7
2,2 = (-1 4-(-2 3)) = 2
2,3 = -(-1 5-(-2 2)) = 1
3,1 = (2 (-2)-(-1 3)) = -1
3,2 = -(-1 (-2)-2 3) = 4
3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу
можно записать как:
| A-1 = |
| 0,6 | -0,4 | 0,8 |
| 0,7 | 0,2 | 0,1 |
| -0,1 | 0,4 | -0,3 |
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы.
- Находим алгебраические дополнения ко всем элементам матрицы.
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы.
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай: Обратной, по отношению к единичной матрице, является единичная матрица.
Пример №2. Найти матрицу, обратную матрице 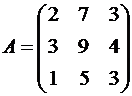 .
.
Решение.
1. Найдем  .
.
2. Ищем алгебраические дополнения каждого элемента матрицы A:  ;
;  ;
;  .
.
Получили алгебраические дополнения элементов первой строки.
Найти обратную матрицу онлайн
Аналогично для элементов второй и третьей строк получаем:  ;
;  ;
;  .
. 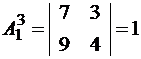 ;
; 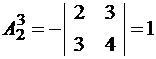 ;
;  .
.
Объединяя 3 и 4 пункты, получаем обратную матрицу  .
.
Для проверки убедимся, что A-1A = E.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу.
Нахождение обратной матрицы
Матрица А-1 называется обратной матрицей по отношению к матрице, если А*А-1 = , где - единичная матрица -го порядка. Обратная матрица может существовать только для квадратных матриц.
Назначение сервиса. С помощью данного сервиса в онлайн режиме можно найти алгебраические дополнения, транспонированную матрицу AT, союзную матрицу и обратную матрицу. Решение проводится непосредственно на сайте (в онлайн режиме) и является бесплатным. Результаты вычислений оформляются в отчете формата Word и в формате Excel (т.е. имеется возможность проверить решение). см. пример оформления.
Нахождение обратной матрицы онлайн
см. также Обратная матрица методом Жордано-Гаусса
Алгоритм нахождения обратной матрицы
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Нахождение транспонированной матрицы AT.
- Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Следующий алгоритм нахождения обратной матрицы аналогичен предыдущему за исключением некоторых шагов: сначала вычисляются алгебраические дополнения, а затем определяется союзная матрица.
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Определение алгебраических дополнений.
- Заполнение союзной (взаимной, присоединённой) матрицы.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент присоединённой матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Пример №1. Запишем матрицу в виде:
Обратная матрица существует, если определитель матрицы отличен от нуля. Найдем определитель матрицы:
= -1 (-1 4-(-2 5))-2 (2 4-(-2 (-2)))+3 (2 5-(-1 (-2))) = 10. Определитель равен 10 и не равен нулю. Продолжаем решение.
Найдем транспонированную матрицу:
Алгебраические дополнения.
1,1 = (-1 4-5 (-2)) = 6
1,2 = -(2 4-(-2 (-2))) = -4
1,3 = (2 5-(-2 (-1))) = 8
2,1 = -(2 4-5 3) = 7
2,2 = (-1 4-(-2 3)) = 2
2,3 = -(-1 5-(-2 2)) = 1
3,1 = (2 (-2)-(-1 3)) = -1
3,2 = -(-1 (-2)-2 3) = 4
3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу
можно записать как:
| A-1 = |
| 0,6 | -0,4 | 0,8 |
| 0,7 | 0,2 | 0,1 |
| -0,1 | 0,4 | -0,3 |
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы.
- Находим алгебраические дополнения ко всем элементам матрицы.
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы.
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Для проверки убедимся, что A-1A = E.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу.
Нахождение обратной матрицы является важной составляющей в разделе линейной алгебры. С помощью таких матриц, если они существуют, можно быстро найти решение системы линейных уравнений.
Матрицаназывается обратной к матрице,если выполняются следующие равенства.
Если определитель матрицыотличен от нуля, то матрицу называют не особо или невырожденной.
Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной
Алгоритм нахождения обратной матрицы
Пусть имеем квадратную матрицу
и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:
1. Найти определитель матрицы. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
2. Найти алгебраические дополнения элементов матрицы . Они равны минорам, умноженным на в степени суммы строки и столбца, для которого ищем.
3. Составить матрицу из алгебраических дополнений элементов матрицы матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается .
4. Разделить присоединенную матрицу на детерминант . Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
Найти матрицу, обратную к матрице (Дубовик В.П., Юрик И.И.
Нахождение обратной матрицы
"Высшая математика. Сборник задач")
1)Находим определитель матрицы
Так как детерминант не равен нулю (), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений
Матрица дополнений примет вид
Транспонируем ее и получаем присоединенную
Разделим ее на определитель и получим обратную
Видим, что в случае, когда определитель равен единице присоединена и обратная матрицы совпадают.
2) Вычисляем определитель матрицы
Находим матрицу алгебраических дополнений
Конечный вид матрицы дополнений
Транспонируем ее и находим союзную матрицу
Находим обратную матрицу
3) Вычислим детерминант матрицы. Для этого разложим его на первую строчку. В результате получим два отличны от нуля слагаемые
Находим матрицу алгебраических дополнений. Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).
Конечный вид матрицы дополнений следующий
Транспонируем ее и находим присоединенную матрицу
Поскольку определитель матрицы равен единице то обратная матрица совпадает с присоединенной. Данный пример назад.
При вычислениях обратной матрицы типичными являются ошибки связанные с неправильными знаками при вычислении определителя и матрицы дополнений.
Высшая математика » Матрицы и определители » Обратная матрица » Вычисление обратной матрицы с помощью алгебраических дополнений.
![]()
![]()
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}\cdot A=A\cdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{n\times n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $\Delta A\neq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{n\times n}^{*}=\left(A_{ij} \right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=\frac{1}{\Delta A}\cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=\left(\begin{array} {cccc} 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & -1 & -9 & 0 \end{array} \right)$.
Обратная матрица
Так как все элементы четвёртого столбца равны нулю, то $\Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $\Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=\left(\begin{array} {cc} -5 & 7 \\ 9 & 8 \end{array}\right)$.
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$ \Delta A=\left| \begin{array} {cc} -5 & 7\\ 9 & 8 \end{array}\right|=-5\cdot 8-7\cdot 9=-103. $$
Так как $\Delta A \neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
\begin{aligned} & A_{11}=(-1)^2\cdot 8=8; \; A_{12}=(-1)^3\cdot 9=-9;\\ & A_{21}=(-1)^3\cdot 7=-7; \; A_{22}=(-1)^4\cdot (-5)=-5.\\ \end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=\left(\begin{array} {cc} 8 & -9\\ -7 & -5 \end{array}\right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=\left(\begin{array} {cc} 8 & -7\\ -9 & -5 \end{array}\right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$). Используя формулу $A^{-1}=\frac{1}{\Delta A}\cdot {A^{*}}^T$, имеем:
$$ A^{-1}=\frac{1}{-103}\cdot \left(\begin{array} {cc} 8 & -7\\ -9 & -5 \end{array}\right)=\left(\begin{array} {cc} -8/103 & 7/103\\ 9/103 & 5/103 \end{array}\right) $$
Итак, обратная матрица найдена: $A^{-1}=\left(\begin{array} {cc} -8/103 & 7/103\\ 9/103 & 5/103 \end{array}\right)$. Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}\cdot A=E$ или $A\cdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}\cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $\left(\begin{array} {cc} -8/103 & 7/103\\ 9/103 & 5/103 \end{array}\right)$, а в виде $-\frac{1}{103}\cdot \left(\begin{array} {cc} 8 & -7\\ -9 & -5 \end{array}\right)$:
Ответ: $A^{-1}=\left(\begin{array} {cc} -8/103 & 7/103\\ 9/103 & 5/103 \end{array}\right)$.
Пример №3
Найти обратную матрицу для матрицы $A=\left(\begin{array} {ccc} 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end{array} \right)$.
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$ \Delta A=\left| \begin{array} {ccc} 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end{array} \right| = 18-36+56-12=26. $$
Так как $\Delta A\neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:

Составляем матрицу из алгебраических дополнений и транспонируем её:
$$ A^*=\left(\begin{array} {ccc} 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end{array} \right); \; {A^*}^T=\left(\begin{array} {ccc} 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end{array} \right) $$
Используя формулу $A^{-1}=\frac{1}{\Delta A}\cdot {A^{*}}^T$, получим:
$$ A^{-1}=\frac{1}{26}\cdot \left(\begin{array} {ccc} 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end{array} \right)= \left(\begin{array} {ccc} 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end{array} \right) $$
Итак, $A^{-1}=\left(\begin{array} {ccc} 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end{array} \right)$. Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}\cdot A=E$ или $A\cdot A^{-1}=E$. Проверим выполнение равенства $A\cdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $\left(\begin{array} {ccc} 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end{array} \right)$, а в виде $\frac{1}{26}\cdot \left(\begin{array} {ccc} 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end{array} \right)$:
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=\left(\begin{array} {ccc} 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end{array} \right)$.
Пример №4
Найти матрицу, обратную матрице $A=\left(\begin{array} {cccc} 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end{array} \right)$.
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
Определитель матрицы $A$ вычислим по следующей формуле:
$$ \Delta A=a_{11}\cdot A_{11}+a_{12}\cdot A_{12}+a_{13}\cdot A_{13}+a_{14}\cdot A_{14}=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

Матрица из алгебраических дополнений: $A^*=\left(\begin{array}{cccc} 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end{array}\right)$.
Присоединённая матрица: ${A^*}^T=\left(\begin{array} {cccc} 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end{array}\right)$
Обратная матрица:
$$ A^{-1}=\frac{1}{100}\cdot \left(\begin{array} {cccc} 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end{array} \right)= \left(\begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end{array} \right) $$
Проверка:

Следовательно, обратная матрица найдена верно.
Ответ: $A^{-1}=\left(\begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end{array} \right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
![]()
![]()
Онлайн-занятия по высшей математике
Нахождение обратной матрицы
Матрица А-1 называется обратной матрицей по отношению к матрице, если А*А-1 = , где - единичная матрица -го порядка. Обратная матрица может существовать только для квадратных матриц.
Назначение сервиса. С помощью данного сервиса в онлайн режиме можно найти алгебраические дополнения, транспонированную матрицу AT, союзную матрицу и обратную матрицу. Решение проводится непосредственно на сайте (в онлайн режиме) и является бесплатным. Результаты вычислений оформляются в отчете формата Word и в формате Excel (т.е. имеется возможность проверить решение). см. пример оформления.
см. также Обратная матрица методом Жордано-Гаусса
Алгоритм нахождения обратной матрицы
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Нахождение транспонированной матрицы AT.
- Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Следующий алгоритм нахождения обратной матрицы аналогичен предыдущему за исключением некоторых шагов: сначала вычисляются алгебраические дополнения, а затем определяется союзная матрица.
- Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
- Вычисление определителя матрицы. Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
- Определение алгебраических дополнений.
- Заполнение союзной (взаимной, присоединённой) матрицы.
- Составление обратной матрицы из алгебраических дополнений: каждый элемент присоединённой матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.
- Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.
Пример №1. Запишем матрицу в виде:
Обратная матрица существует, если определитель матрицы отличен от нуля. Найдем определитель матрицы:
= -1 (-1 4-(-2 5))-2 (2 4-(-2 (-2)))+3 (2 5-(-1 (-2))) = 10. Определитель равен 10 и не равен нулю. Продолжаем решение.
Найдем транспонированную матрицу:
Алгебраические дополнения.
1,1 = (-1 4-5 (-2)) = 6
1,2 = -(2 4-(-2 (-2))) = -4
1,3 = (2 5-(-2 (-1))) = 8
2,1 = -(2 4-5 3) = 7
2,2 = (-1 4-(-2 3)) = 2
2,3 = -(-1 5-(-2 2)) = 1
3,1 = (2 (-2)-(-1 3)) = -1
3,2 = -(-1 (-2)-2 3) = 4
3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу
можно записать как:
| A-1 = |
| 0,6 | -0,4 | 0,8 |
| 0,7 | 0,2 | 0,1 |
| -0,1 | 0,4 | -0,3 |
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы.
- Находим алгебраические дополнения ко всем элементам матрицы.
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы.
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Для проверки убедимся, что A-1A = E.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу.
Похожие на обратные по многим свойствам.
Энциклопедичный YouTube
1 / 5
✪ Обратная матрица (2 способа нахождения)
✪ Как находить обратную матрицу - bezbotvy
✪ Обратная матрица #1
✪ Решение системы уравнений методом обратной матрицы - bezbotvy
✪ Обратная Матрица
Субтитры
Свойства обратной матрицы
- det A − 1 = 1 det A {\displaystyle \det A^{-1}={\frac {1}{\det A}}} , где det {\displaystyle \ \det } обозначает определитель .
- (A B) − 1 = B − 1 A − 1 {\displaystyle \ (AB)^{-1}=B^{-1}A^{-1}} для двух квадратных обратимых матриц A {\displaystyle A} и B {\displaystyle B} .
- (A T) − 1 = (A − 1) T {\displaystyle \ (A^{T})^{-1}=(A^{-1})^{T}} , где (. . .) T {\displaystyle (...)^{T}} обозначает транспонированную матрицу.
- (k A) − 1 = k − 1 A − 1 {\displaystyle \ (kA)^{-1}=k^{-1}A^{-1}} для любого коэффициента k ≠ 0 {\displaystyle k\not =0} .
- E − 1 = E {\displaystyle \ E^{-1}=E} .
- Если необходимо решить систему линейных уравнений , (b - ненулевой вектор) где x {\displaystyle x} - искомый вектор, и если A − 1 {\displaystyle A^{-1}} существует, то x = A − 1 b {\displaystyle x=A^{-1}b} . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса-Жордана
Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 {\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}} . Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 − a m − 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 − a m + 1 m / a m m 1 … 0 … 0 … 0 − a n m / a m m 0 … 1 ] {\displaystyle \Lambda _{m}={\begin{bmatrix}1&\dots &0&-a_{1m}/a_{mm}&0&\dots &0\\&&&\dots &&&\\0&\dots &1&-a_{m-1m}/a_{mm}&0&\dots &0\\0&\dots &0&1/a_{mm}&0&\dots &0\\0&\dots &0&-a_{m+1m}/a_{mm}&1&\dots &0\\&&&\dots &&&\\0&\dots &0&-a_{nm}/a_{mm}&0&\dots &1\end{bmatrix}}} .Вторая матрица после применения всех операций станет равна Λ {\displaystyle \Lambda } , то есть будет искомой. Сложность алгоритма - O (n 3) {\displaystyle O(n^{3})} .
С помощью матрицы алгебраических дополнений
Матрица, обратная матрице A {\displaystyle A} , представима в виде
A − 1 = adj (A) det (A) {\displaystyle {A}^{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj (A) {\displaystyle {\mbox{adj}}(A)} - присоединенная матрица ;
Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .
Использование LU/LUP-разложения
Матричное уравнение A X = I n {\displaystyle AX=I_{n}} для обратной матрицы X {\displaystyle X} можно рассматривать как совокупность n {\displaystyle n} систем вида A x = b {\displaystyle Ax=b} . Обозначим i {\displaystyle i} -ый столбец матрицы X {\displaystyle X} через X i {\displaystyle X_{i}} ; тогда A X i = e i {\displaystyle AX_{i}=e_{i}} , i = 1 , … , n {\displaystyle i=1,\ldots ,n} ,поскольку i {\displaystyle i} -м столбцом матрицы I n {\displaystyle I_{n}} является единичный вектор e i {\displaystyle e_{i}} . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) .
Если матрица A невырождена, то для неё можно рассчитать LUP-разложение P A = L U {\displaystyle PA=LU} . Пусть P A = B {\displaystyle PA=B} , B − 1 = D {\displaystyle B^{-1}=D} . Тогда из свойств обратной матрицы можно записать: D = U − 1 L − 1 {\displaystyle D=U^{-1}L^{-1}} . Если умножить это равенство на U и L то можно получить два равенства вида U D = L − 1 {\displaystyle UD=L^{-1}} и D L = U − 1 {\displaystyle DL=U^{-1}} . Первое из этих равенств представляет собой систему из n² линейных уравнений для n (n + 1) 2 {\displaystyle {\frac {n(n+1)}{2}}} из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для n (n − 1) 2 {\displaystyle {\frac {n(n-1)}{2}}} из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA) −1 = A −1 P −1 = B −1 = D. получаем равенство A − 1 = D P {\displaystyle A^{-1}=DP} .
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма - O(n³).
Итерационные методы
Методы Шульца
{ Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i {\displaystyle {\begin{cases}\Psi _{k}=E-AU_{k},\\U_{k+1}=U_{k}\sum _{i=0}^{n}\Psi _{k}^{i}\end{cases}}}
Оценка погрешности
Выбор начального приближения
Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору U 0 {\displaystyle U_{0}} , обеспечивающие выполнение условия ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы A A T {\displaystyle AA^{T}} (а именно, если A - симметричная положительно определённая матрица и ρ (A) ≤ β {\displaystyle \rho (A)\leq \beta } , то можно взять U 0 = α E {\displaystyle U_{0}={\alpha }E} , где ; если же A - произвольная невырожденная матрица и ρ (A A T) ≤ β {\displaystyle \rho (AA^{T})\leq \beta } , то полагают U 0 = α A T {\displaystyle U_{0}={\alpha }A^{T}} , где также α ∈ (0 , 2 β) {\displaystyle \alpha \in \left(0,{\frac {2}{\beta }}\right)} ; можно конечно упростить ситуацию и, воспользовавшись тем, что ρ (A A T) ≤ k A A T k {\displaystyle \rho (AA^{T})\leq {\mathcal {k}}AA^{T}{\mathcal {k}}} , положить U 0 = A T ‖ A A T ‖ {\displaystyle U_{0}={\frac {A^{T}}{\|AA^{T}\|}}} ). Во-вторых, при таком задании начальной матрицы нет гарантии, что ‖ Ψ 0 ‖ {\displaystyle \|\Psi _{0}\|} будет малой (возможно, даже окажется ‖ Ψ 0 ‖ > 1 {\displaystyle \|\Psi _{0}\|>1} ), и высокий порядок скорости сходимости обнаружится далеко не сразу.
Примеры
Матрица 2х2
Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \mathbf{A}^{-1} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}^{-1} = \frac{1}{\det(\mathbf{A})} \begin& \!\!-b \\ -c & \,a \\ \end{bmatrix} = \frac{1}{ad - bc} \begin{bmatrix} \,\,\,d & \!\!-b\\ -c & \,a \\ \end{bmatrix}.}Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .